Determine Which Function Produces the Same Graph as

Determine which of the following vector. All you need to put is the two equations and the values of t you want to display.

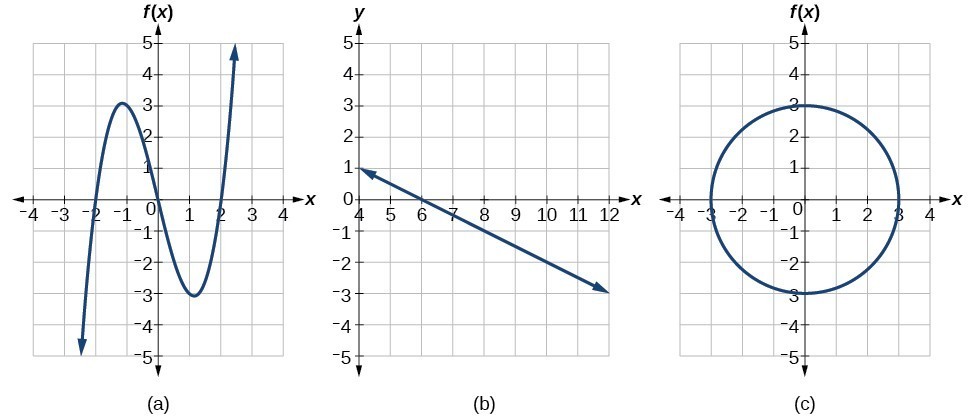
Identify Functions Using Graphs College Algebra

Hx 3x55x33 h x 3 x 5 5 x 3 3.

. Give reason for your answers concerning each graph. Solving can produce more than one solution because different input values can produce the same output value. If the vertical line intersects the graph in at most one point then the given graph represents a function.

Determine whether a function is one-to-one. Function notation gives you more flexibility because you dont have to use y for every equation. 5x 8 3x 10 Consider the functions shown on the graph.

It represents the following situation. Each of the vector functions fall into one of three groups. For example in the following stock chart the stock price.

A function named f acts upon an input x and produces fx which is equal to 4x 1. The initial value of the function is 1The rate of the function is 42 or 16. The fact that each input value has exactly one output value means graphs of functions have certain characteristics.

Determine whether a function is one-to-one. Find the points where the line rt 4t-6 6-1 -2t4 intersects the ellipsoid r 4y z 8. The graph of the function is the graph of all ordered pairs.

Which of the following vector-valued functions represent the same graph. Correct answer to the question Determine which function produces the same graph as f1 181 16. Creating a graph of a function is one way to understand the relationship between the inputs and outputs of that function.

Determine whether the graph given below represent functions. Inspect the graph to see if any vertical line drawn would intersect the curve more than once. The procedure for secant is very similar because the cofunction identity means that the secant graph is the same as the cosecant graph shifted half a period to the left.

Some functions have a given output value that corresponds to two or more input values. Given a graph use the vertical line test to determine if the graph represents a function. Equations on One Side flashcards containing study terms like Which input value produces the same output value for the two functions on the graph.

Determine which of the following vector functions will produce the same graph. So it looks like this-. Use this information to sketch the graph.

F x 2 x 3. This can be a helpful way to distinguish equations of functions when you are. We said that the relation defined by the equation.

When both the independent quantity input and the dependent quantity output are real numbers a function can be represented by a graph in the coordinate plane. Select all that apply r t -8 cos t 2i 9 sint t 3j 2k r t 2i -8 cos t 2j 9 sin t 3k r t 8 cos t - 2i -9 sin t - 3j 2k r t -8 cos 2t 2i 9 sin 2t 3j 2k. F x 2 x 3.

For example if you only want to graph the part of the ellipse in Sals example at the beginning of the video you put the equations and the values of t. Memorize flashcards and build a practice test to quiz yourself before your exam. It is your job to group them according to their graph.

Vertical and phase shifts may be applied to the cosecant function in the same way as for the secant and other functions. The equations become the following. For example the black dots on the graph in the graph below tell us that latexfleft0right2latex and latexfleft6right1latex.

This is the same as the equation as y 4x 1. Creating a graph can be done by choosing values for x finding the corresponding y values and plotting them. The function may be able to be written in a variety of ways but it is really the same function.

The independent value is plotted on the x-axis and the dependent value is plotted on the y-axis. These three functions will all produce the same graph because they are really all the same function just written differently. Lets take the following quadratic functions.

If there is any such line the graph does not represent a function. Which function will produce the same graph as the function shown below. See attachment for the complete solution.

The function that produces the same graph is. We can write this as in function notation as. We have to check whether the vertical line drawn on the graph intersects the graph in at most one point.

A curve drawn in a graph represents a function if every vertical line intersects the curve in at most one point. Y 2 x 3. Example 1 For the following function identify the intervals where the function is increasing and decreasing and the intervals where the function is concave up and concave down.

Knowing the effect of changes to the basic function equation is also helpful. If no vertical line can intersect the curve more than once the graph does represent a function. Start studying the Solving Linear Equations.

It still means the same thing. If the function is defined for only a few input values then the graph of the function is only a few points where the x-coordinate of each point is an input value and the y-coordinate of each point is the corresponding output value. Y x - 1 x - 3 Multiple answers may be correct.

Y 2 x 3 is a function. Draw a vertical line at any where on the given graph. Lets take a look at an example of that.

An exponential function is represented as. Instead you could use fx or gx or cx. If I expand distribute and simplify I will get.

However it helps to understand the basic shape of the function. A represents the initial valueb represents the rate. Since the graph intersects the vertical line y-axis at two points it is not a function.

Y 2 x 3 and its graph as we developed the vertical line test. A t t e 92 b tt t 0 f sint sint c tt Question. X 1 x 0 x 1 x 2 Solve the equation.

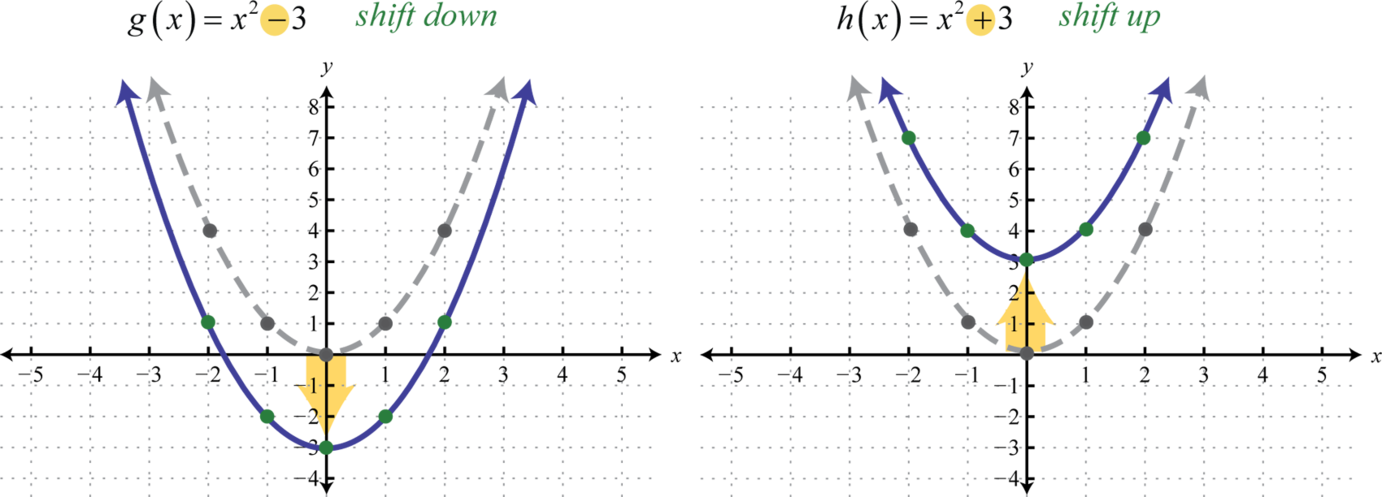
Using Transformations To Graph Functions

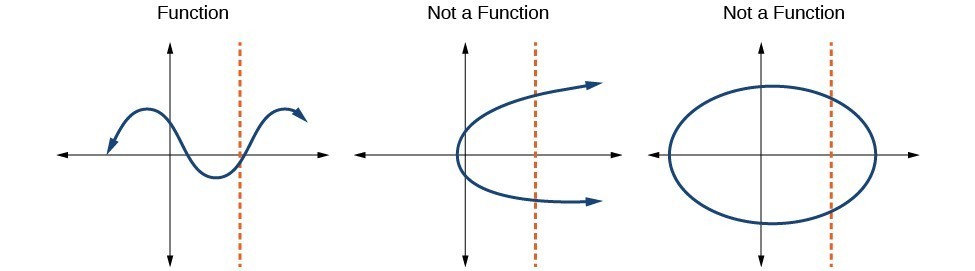
Identify Functions Using Graphs College Algebra

What Makes A Graph A Function Quora

Identify Functions Using Graphs College Algebra